新機能で Lambda を採用するために検討したこと
この記事は「弁護士ドットコム Advent Calendar 2022」の 14日目の記事です。 昨日は @shellme さんでした。
はじめに
こんにちは。 弁護士ドットコム株式会社のクラウドサイン事業本部で、スクラムマスターをしながらバックエンドの開発に携わっている @enkdsn です。
クラウドサインではアプリケーションの実行に多くの ECS on Fagate を使っており、メインとなるサービスのほかにバッチ処理を行うサービスが多く存在しています。 しかし、Fagate のコストは地味に高く、マネージドであることのコストを差し引いてもそれなりに痛いものになります。 そこで「ECS on Fagate ではなく Lambda を使うことでコストを節約していけるか」ということで、新しい機能開発で Lambda を採用するに至った話をできればと思います。
この記事で言及すること
- Lambda vs ECS を検討するに至った背景
- Lambda を選ぶために考慮したこと
- Lambda の開発環境
この記事で言及しないこと
- Runtime Interface Emulator(RIE) の使い方
- 新機能のアーキテクチャ
- 具体的な開発環境の構築方法
Lambda vs ECS を検討するに至った背景
クラウドサインでは ECS のクラスタ内で起動するタスクが多く存在しており、新機能で worker や cron が必要になった場合は ECS のクラスタに追加されていきます。それによりコスト面での問題が発生しつつあります。
伸びゆく ECS のコスト
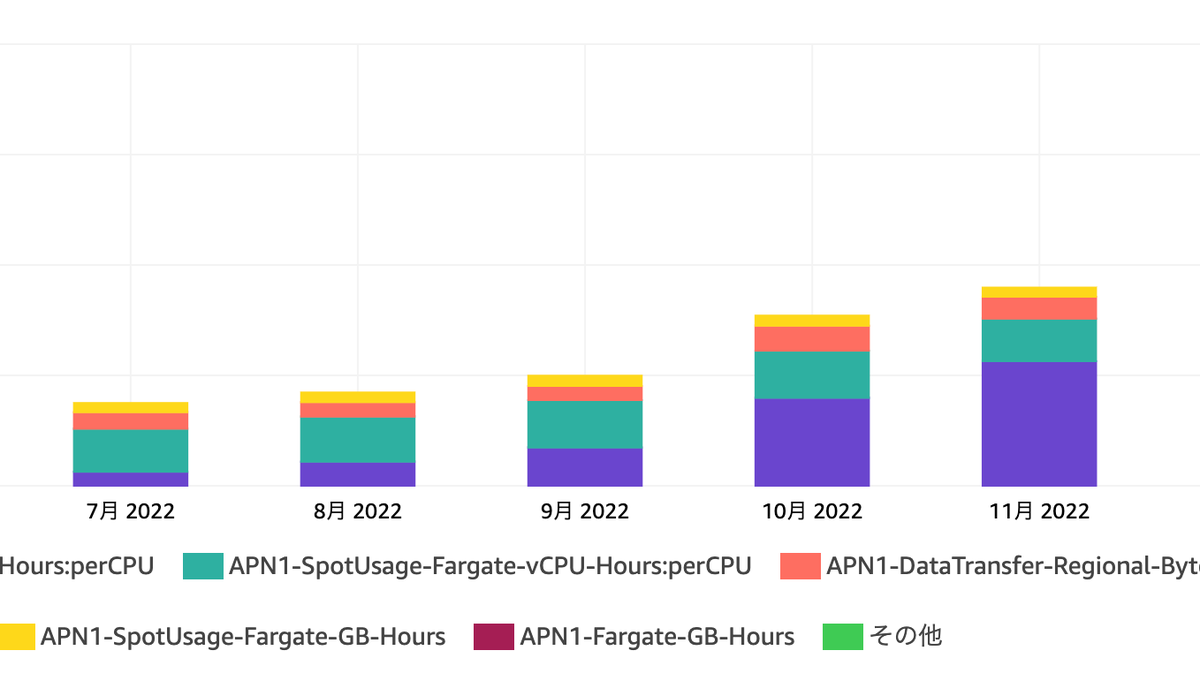
画像の通り、クラウドサイン内での ECS における vCPU の課金額が直近右肩上がりで上昇しています。 この要因として、クラウドサイン内で動くタスク数が増えてきているということが挙げられます。タスク数増加の背景は、クラウドサインが社会インフラとしての責任を果たすにあたり高可用性が求められるようになることへの備えをはじめたことにあります。これによって疎結合なアーキテクチャを取り入れるようになり、各所で非同期のワーカーサービス等が立つようになりました。
ECS クラスタに worker や cron の多くが追加される背景
これは、クラウドサイン内での Lambda での開発事例の少なさと ECS での worker, cron の実績の多さにあると個人的に感じています。
クラウドサインでは、Lambda を採用した機能の事例があまり多くありませんでした。採用事例が少ない背景について明確な理由は見いだせていないですが、おそらく Lambda でのローカル開発の体験がコンテナのそれに劣っていたからということがあるかと個人的に考えています。私自身も SAM に慣れておらず、Lambda での開発は若干敬遠しているところがありました。
ECS であれば既存の worker や cron の Dockerfile や docker-compose.yml、.tf を使い回せていたため、わざわざ Lambda での開発環境を整えるよりもアプリケーションに集中しやすい状態でした。
しかし、そろそろ Faragate のコストも無視できなくなってきており、適切なユースケースがあれば Lambda を採用する必要が出てきました。このコストの問題はクラウドサインの SRE チームから掲示され、アプリケーション開発者もコスト面を意識するようになりました。これをきっかけに、私が参加しているチームではその流れに乗っかろうということで Lambda 採用を検討するに至りました。
Lambda を選ぶために考慮したこと
実際に Lambda を採用するためにいくつかの検討を行いました。 具体的には以下 3 点の確認・検討を行いました。
- ユースケースの特性の確認
- コンテナと Lambda の比較による検討
- Lambda を採用するための追加検討
ユースケースの特性の確認
まず、新機能でのユースケースの確認をしました。新機能の特性は以下のようなものです。
- この機能の使用頻度はそこまで多くない(四半期に1度この機能を複数回利用することを想定)
- この機能のレスポンスタイムは短くなくてもよい(20秒くらいでも問題ないと想定)
- この機能は一つのフロー上で完結させたい。つまり、"見かけ"は同期的である必要がある。*1
以上を踏まえると、
- ECS で worker を動かす場合はコスパが悪い
- 多少コンピューティングリソースが少なくてもよい
- ユーザーフローは同期的にしたいので cron は採用しづらい
ということが考えられます。
すでに Lambda を採用すべきように見えますが検討を続けます。
AWS で提案されているディシジョンツリーの確認
ユースケースの確認によって、Lambda でいけそうというアタリをつけることができました。 次に、AWS で提案されているコンテナと Lambda のディシジョンツリーの確認をしました。
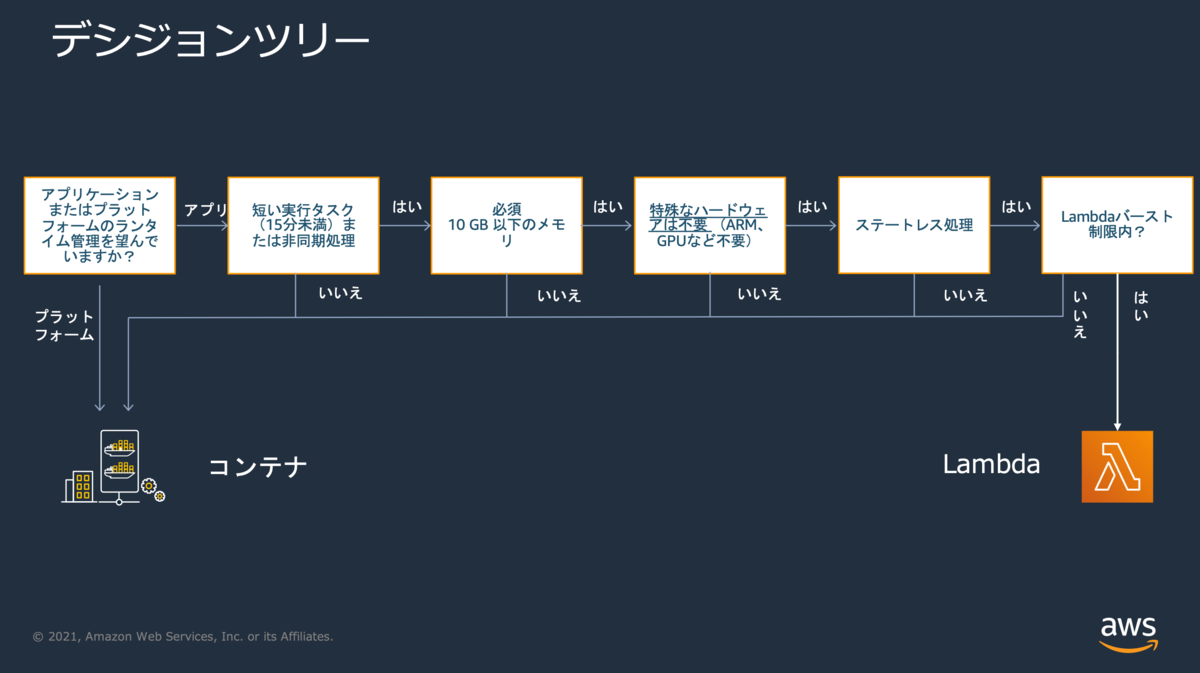
ここでは以下の観点でディシジョンツリーを下っていきます。
- アプリケーションまたはプラットフォームのランタイム管理を望んでいますか?
- 短い実行タスク(15分未満)または非同期処理ですか?
- 使用するメモリは 10 GB 以下ですか?
- 特殊なハードウェアは不要ですか?
- ステートレス処理ですか?
- Lambdaバースト制限内ですか?
雑に回答を作るとこんな感じでしょうか
| Q | A | |
|---|---|---|
| 1 | アプリケーションまたはプラットフォームのランタイム管理を望んでいますか? | ランタイム管理は不要 |
| 2 | 短い実行タスクまたは非同期処理? | Yes - 非同期であり、想定実行時間は長くて1分 |
| 3 | 10 GB 以下のメモリ? | Yes - サービス仕様としてデータ数上限がある |
| 4 | 特殊なハードウェアは不要? | Yes |
| 5 | ステートレス? | Yes |
| 6 | Lambdaバースト制限内? | Yes - 同時実行クォータが 1000 (ap-northeast-1) あるので問題なし。ただし、VPC Lambda の予定なので ENI クォータ 250 を使い切らないことにも注意。 |
ディシジョンツリーを踏まえても Lambda で問題ないことがわかりました。
Lambda を採用するための追加検討
先述した検討を踏まえて、概ね Lambda でいいだろうという方針になりました。 ここから、技術的な要件に問題はないかについて検討をしました。
冪等性・排他制御
冪等性を担保することができそうか
Lambda は自動でリトライがありこれが大変便利なので、冪等性を担保できるか検討しました。 新機能ではマスターデータを元にデータベースを更新するということが求められていました。これは「何度実行してもデータベースをマスターデータが想定している状態にする」と考えることもでき、このようにアプリケーションを実装することで冪等性を担保できそうです。 経験上 Lambda のエラーでよく遭遇したのは一時的な DB のコネクションタイムアウトで、このエラーはリトライするとたいてい成功しますので、障害要因が一時的なものについては自動リトライで済ますという運用ができてかなり楽ができます。
排他制御はどうするか
先に述べたとおり「マスターデータを元にデータベースを更新する」ということを想定していたわけですが、同時実行による問題があるかについても検討しました。 たとえば、ユーザーAとユーザーBが、内容が部分一致するマスターデータを同時に一括処理に投げたらというケースなどです。 「レコードが作られたかどうか」だけに着目すれば、ユーザーAが投げたデータとユーザーBが投げたデータの和集合を正とすることで問題ないですが、期待値と実行結果がプレビューと異なるようなことはなるべく避けたいという要望もあり、同時実行をさせないようにする方針にしました。
これは、以下2つの方針をあわせることで実現することにしました。
* SQS の MessageGroupID を使用して同時実行を制限するようにする
* 一括処理を管理するテーブルにて複合ユニークキーを貼ることで同時実行を防ぐ*2
厳密な排他制御は、後者の複合ユニーク制約によって実現されます。Lambda 起動後にまずレコードを更新し、その際に複合ユニークキーを貼ったカラムを更新します。もし別の Lambda が起動した場合はユニーク制約に引っかかり起動できません。加えて MessageGroupID による重複排除を行うことで、特定のチームに対する更新処理で Lambda の同時実行が発生しないようにしました。
RDS Proxy
Lambda を論じるにあたりよく言及される RDS Proxy ですが、今回は採用しなくてもよいだろうということになりました。 採用を見送った理由は以下です。
接続プーリングをあまり必要としていなかった
そもそも Lambda * RDS の相性が悪いとされる原因として、Lambda がデータベースのコネクションを使い潰してしまうということが言われていました。それを解消すべく提案されたのが RDS Proxy ですが、今回開発している新機能は高頻度で使われることを想定していません。したがって、Lambda の同時実行数が急激に伸びることでコネクションを使い潰してしまうことを想定しなくてもよいということで RDS Proxy の恩恵を受けづらいということがわかりました。*3
RDS Proxy が高い
安ければ接続プーリングができるし採用してもいいかなと思いました。 しかし、RDS Proxy を採用すると Lambda にしたコストメリットを潰してしまいかねないくらいに高くなりそうという見込みになりました。 Amazon RDS プロキシの料金 | 高可用性データベースプロキシ | Amazon Web Services
料金例にある通り、「RDS プロキシの料金は、Aurora クラスターの各データベースインスタンスの vCPU 数に相関します。」となっているので、大規模なサービスだと相当な額になります。今回の機能開発では Writer インスタンスにも Reader インスタンスにも接続する可能性があったため、例にあるとおり 43.20 USD かかる可能性もありました。これでは Lambda にすることで節約したコストを大きく上回る可能性があり、RDS Proxy を採用しないことにしました。
EFS
クラウドサインでは EFS を利用する必要がある場面があり、今回の新機能開発においても EFS が利用できる必要がありました。 実際はマウントは問題なくできることが分かったため、これについてもクリアになりました。
マウントにかかる時間や IOPS などについて細かく調べることはしませんでした。調べても出てこなかったのと、マウントポイントを介してアクセスするところは ECS on Fargate も共通であり、Lambda であることで大きなデメリットを抱えることはないという予想のもとです。*4
Lambda のトリガー
今回はマスターデータを S3 に保存するので、S3 の Put イベントをトリガーにするという方針も取れましたが、以下を理由に SQS にしました。
- マスターデータの他に必要なメタデータが存在する
- MessageGroupID による同時実行制御の必要性
前者は SQS のメッセージにメタデータを埋めることで解決させる必要がありました。また、排他制御の項で言及したMessageGroupID同時実行の制限もできれば欲しかったので、今回は SQS のメッセージングをトリガーにすることにしました。
Lambda 採用を後押ししてくれたもの
「Lambda を採用するための追加検討」の部分で技術的な要件を満たせることも確認できたのですが、根本の問題だった「開発環境」が解決していませんでした。納期や開発者体験を優先すれば ECS でもよかったのですが、Lambda のコンテナイメージのサポートや同時に出た Runtime Interface Emulater を使用することで開発者体験を損なわないことがわかりました。
コンテナイメージのサポート
もう2年前にはなりますが、Lambda はコンテナイメージをサポートするようになりました。 余談ですが、サポートした背景として、コンテナツールに投資した場合の Lambda アプリケーションの構築について言及されており、先述した Lambda が採用されづらかった背景に通ずるものがあるなと感じました。
AWS Lambda では、サーバーについて気にすることなくコードをアップロードして実行できます。多くのお客様に Lambda のこの仕組みをご活用いただいていますが、開発ワークフローのためにコンテナツールに投資した場合は、Lambda でのアプリケーションの構築に同じアプローチを使用することが難しくなります。
https://aws.amazon.com/jp/blogs/news/new-for-aws-lambda-container-image-support/
コンテナイメージのサポートによって docker compose のエコシステムを使って開発できるようになり、アプリケーションの構築方法の差を気にしなくてよくなりました。 Dockerfile を書いて、docker-compose.yml を書いて、Lambda をエミュレートするコンテナを立ち上げたらそこへ curl をすれば Lambda が起動するといった流れは、いままでのコンテナによる開発と遜色ありません。 実際の開発では、nats に流れてきたメッセージを吸って curl するデーモンを起動しておくようにしているので、デーモンの起動と Lambda のコンテナを docker compose up すれば動作するようになっています。Localstack を使うという選択肢もありますが、SQS をトリガーにしている都合で Localstack は Pro にしないといけなくなり、加えて不便さを感じていないのでこの形に落ち着いています。
まとめ
以上の検討を経て、実際に Lambda を採用し実際に新機能開発を進めています。
まだリリースされていない機能であるため、実際にコストがどれくらい軽減されたのか等は今後判明することになりますが、きっと安くなるでしょう。(それは来年のアドベントカレンダーに書かれるかもしれないし書かれないかもしれない。)
開発者体験の問題についても、Lambda がコンテナイメージに対応したおかげで今までのコンテナによる開発と遜色なく、キャッチアップのコストがかなり少なく済んだと実感しています。
Lambda やそのまわりのエコシステムの進化によって「コンテナ開発は ECS/EKS」という認識はとうに過去のものになっていると感じさせられました。サービス数が増えつつあるなかで、アーキテクチャを検討する上で Lambda vs ECS を考慮する機会は多く存在すると思います。少しでも参考になったら嬉しいです。 それではみなさま、よきサーバーレスライフを。
明日は @dskymd さんです。お楽しみに。
参考文献
AWS Lambda の新機能 – コンテナイメージのサポート | Amazon Web Services ブログ
Amazon SQSメッセージ重複排除ID の使用 - Amazon Simple Queue Service
Lambda で Amazon EFS を使用する - AWS Lambda
*1:ここでいう”見かけ"は同期的という表現ですが、画像アップロードでいう「アップロード→ローディング→完了」のように、ローディングをはさみつつユーザーへの操作を継続させたいという意図を持ったフローを意味しています
*2:ここで複合ユニークキーとしているのは、チーム内での排他制御を実現するためです。もし全体で一つの処理しかしないのであれば単一のユニークキーで問題ないです。
*3:もし RDS Proxy を"使わない"場合、コネクションの切断はコード側から明示的に行う必要があります。VM が落ちるまでは DB とつながりっぱなしになり、一定期間コネクションが右肩上がりになって上限に近づいていくモニタを見ると震えます。単一の DB でサービスを動かしている場合は、Lambda でコネクションを切らなかったばかりにメインとなるサービスを落としてしまうこともあるので十分に注意してください。
*4:あくまで予想のですので、もし問題があった場合は追記します。
コンテナで動くGoのバイナリを安全に葬りたい
今年の11月からクラウドサインで主にバックエンドをやっている@enkdsnです。
この記事は弁護士ドットコム Advent Calendar 2020、13日目の記事です。 昨日は同じチームの@michimaniさんでした。これを読んではてなブログから移行したい。
はじめに
クラウドサインでは現在、サービス基盤のコンテナ化とECSへの移行を進めています。 そんな中、ECSのタスク更新時に起きていることを確認すると、シグナルハンドリングやったほうがいいなという気付きがありました。
Amazon Elastic Container Service 開発者ガイド サービスの更新 より引用
更新中にサービススケジューラがタスクを置き換えるとき、サービスはまずロードバランサーからタスクを削除し (使用されている場合)、接続のドレインが完了するのを待ちます。その後、タスクで実行されているコンテナに docker stop と同等のコマンドが発行されます。この結果、SIGTERM 信号と 30 秒のタイムアウトが発生し、その後に SIGKILL が送信され、コンテナが強制的に停止されます。コンテナが SIGTERM 信号を正常に処理し、その受信時から 30 秒以内に終了する場合、SIGKILL 信号は送信されません。サービススケジューラは、最小ヘルス率と最大ヘルス率の設定で定義されているとおりに、タスクを開始および停止します。
これはECSで動かす場合に限らず、コンテナの上でアプリケーションを動かす場合は等しく意識すべきかと思います。ですので今回は、docker stopした際にGoのバイナリがいろいろ終了処理をやったあと正常に終了できるように、SIGTERMを拾って終了処理ができるよう実装していきたいと思います。
前提:30秒の猶予でやりたいこと
実装に入る前に、まず終了処理で何をするべきかという部分について前提を置きます。 コンテナが途中で落ちた場合、処理中のデータのロスト、データ不整合の発生が懸念されます。これを防ぐために、Graceful Shutdownという仕組みがあります。HTTPサーバであれば、新規のリクエストの受付は止めて、すでに受け付けているリクエストはレスポンスを返しきり、そのあとにサーバを終了するといった具合です。これが終了処理が適切にされないままだと、ユーザのリクエスト情報が途中でロストして、データ不整合を起こす可能性があります。
ですから、終了処理においては「処理中のデータをロストしないようにする」という目的を達成する必要があります。では、それを達成するために具体的に何をするべきでしょうか。仮にGoのバイナリを動かすようなシチュエーションの場合、以下のような終了処理が考えられるかと思います。
contextのキャンセルとトランザクションの掃除
SIGTERMを受け取った段階で動いているgoroutineを止めに行きます(contextを伝搬させているもの)。データ不整合などを防ぐためにcontextがキャンセルされたらロールバックを行うような実装をしている場合は、contextのキャンセル通知→キャンセル処理が完了するまで待機とすることで、サービス層の一連の処理を安全に止めることができます。*3
ここで、さらに具体的なケースを考えます。ある処理がトランザクションの内部にいる際にSIGTERMが発行された場合を考えましょう。contextが伝搬された処理のうち、例えば、sqlパッケージのQueryContext()は、内部でgrabConn()というメソッドを呼んでいます。
func (tx *Tx) grabConn(ctx context.Context) (*driverConn, releaseConn, error) { select { default: case <-ctx.Done(): return nil, nil, ctx.Err() }
ここでは伝搬されてきたcontextがキャンセルされていたら空のコネクションを返し、ctx.Err()を返しています。これで、クエリ発行前にコンテキストのキャンセルがあった場合は、コネクションの獲得を途中でキャンセルできます。 また、トランザクションの内部に入ってコミット手前という状況も考えます。
func (tx *Tx) Commit() error { // Check context first to avoid transaction leak. // If put it behind tx.done CompareAndSwap statement, we can't ensure // the consistency between tx.done and the real COMMIT operation. select { default: case <-tx.ctx.Done(): if atomic.LoadInt32(&tx.done) == 1 { return ErrTxDone } return tx.ctx.Err() }
こちらもgrabConnと同様に、contextがキャンセルされていたらエラーを返すようにしています。終了処理としてコンテキストのキャンセルを適切に行うことで、トランザクションの掃除ができます。
DB接続の切断
一通りcontextのキャンセル処理がなされるとDBのコネクションの解放がされているはずです*4。トランザクションが一通り処理され、さらに新しいクエリも受け付けない状態にします。
サーバーのGraceful Shutdown
サーバーのGraceful Shutdownを行い、リクエストとレスポンスの掃除をします。Go1.8からhttpパッケージにGraceful Shutdownの機能が入りましたので、リクエストの終了からコンテキストの掃除まで標準パッケージでできます。Shutdownを起動すれば、Listnerを閉じ、指定したインターバルだけcontextの処理の終了を待つので、上述したcontextのキャンセルよりも綺麗です。
終了処理の例はこれだけでは無いと思いますが、Web界隈でよくあるバッチやサーバーにおける終了処理はこれらが該当するでしょう。
実装
30秒の猶予で何をしたいか整理したので、ここからはシグナルを受け取る実装をしていきます。ただし、終了処理の内部については詳細まで実装していないので悪しからず。
実装1:signal受け取りの簡単な例
まず簡単なサンプルコードからです。雰囲気を手元で確認する場合は割り込みの方が確認しやすいいので、SIGINTを受け取ります。SIGINTを使う実装はCLIツールを割り込みされても正しく終了する時に使えます。(この段階ではWaitGroupが機能してないですが、後の実装でWaitする実装が入るので前もって入れています)
package main import ( "fmt" "os" "os/signal" "sync" "syscall" "time" ) func main() { // 必ず、バッファ付きチャネルを使用する。 sigChan := make(chan os.Signal, 1) defer close(sigChan) signal.Notify(sigChan, syscall.SIGINT) wg := sync.WaitGroup{} wg.Add(1) go func() { defer wg.Done() for { time.Sleep(1 * time.Second) fmt.Println("app running") } }() s := <-sigChan // sigChanからsignalを受け取る switch s { case syscall.SIGINT: fmt.Println("!!! SIGINT detected !!!!") OnAppStop() return default: fmt.Println("unexpected signal") } } // OnAppStop は、アプリの終了前にやるべき処理(DBConnectionの解放とか)を行う func OnAppStop() { fmt.Println("=== 終了処理をいろいろやる ===") fmt.Println("successful termination") }
メインゴルーチンはアプリケーションをゴルーチンで起動した後、signalの受け取りを待ちます。ctrl+cで割り込みがあった際はSIGINTを検出して終了処理(OnAppStop)を起動します。 注意点ですが、今回のようにシグナルハンドラとしてsignalを受け付けるチャネルはバッファ1のバッファ付きチャネルにしてください。*5
Package signal will not block sending to c: the caller must ensure that c has sufficient buffer space to keep up with the expected signal rate. For a channel used for notification of just one signal value, a buffer of size 1 is sufficient.
Notify()のドキュメンテーションコメントにも書いてありますね。
実際に動かし、ctrl+cで割り込みをします。 結果は下記のようになるはずです。
app running app running app running app running ^C!!! SIGINT detected !!!! === 終了処理をいろいろやる === successful termination
ちゃんと終了処理が動いてますね。シグナルを受け取り終了処理が完了するとメインゴルーチンが終了するので、アプリケーションを動かしていたサブ的なゴルーチンも消えます。
実装2:Goのバイナリを実行しているコンテナを止める
つぎに、先ほどのコードを、docker stopされた際に終了処理が行えるようにします。docker stopを打ったあとは、対象のコンテナで起動しているPID=1のプロセスをSIGTERMで止めにきます。検出するシステムコールをSIGINTからSIGTERMに変えました。(この段階ではWaitGroupが機能してないですが、後の実装でWaitする実装が入るので前もって入れています)
package main import ( "fmt" "os" "os/signal" "sync" "syscall" "time" ) func main() { sigChan := make(chan os.Signal, 1) defer close(sigChan) signal.Notify(sigChan, syscall.SIGTERM) wg := sync.WaitGroup{} wg.Add(1) go func() { defer wg.Done() for { time.Sleep(1 * time.Second) fmt.Println("app running") } }() s := <-sigChan switch s { case syscall.SIGTERM: fmt.Println("!!! SIGTERM detected !!!!") OnAppStop() return default: fmt.Println("unexpected signal") } } func OnAppStop() { fmt.Println("=== 終了処理をいろいろやる ===") fmt.Println("successful termination") }
コンテナで動かします。
FROM golang:latest WORKDIR /go/src/sig_test COPY main.go . RUN go install -v CMD ["sig_test"]
コンテナを実行。
$ docker build -t sig_test_docker . $ docker run -d --rm --name sig_test sig_test_docker
動いているかログを確認。大丈夫そうです。
$ docker logs -f sig_test
2020-12-02T04:24:53.306288800Z app running
2020-12-02T04:24:54.306528100Z app running
2020-12-02T04:24:55.307003500Z app running
ここで、docker stopします
docker stop sig_test
するとログには
app running app running !!! SIGTERM detected !!!! === 終了処理をいろいろやる === successful termination
のように表示され、終了処理が正しく動いていることがわかります。
実装3:contextを伝搬させたタスクの処理
さらに拡張させ、contextを伝搬させたタスクを安全に終了させるようにします。 タスクをgoroutineで起動させます。
package main import ( "context" "fmt" "os" "os/signal" "sync" "syscall" "time" ) func main() { sigChan := make(chan os.Signal, 1) defer close(sigChan) signal.Notify(sigChan, syscall.SIGTERM) ctx, cancel := context.WithCancel(context.Background()) defer cancel() wg := sync.WaitGroup{} wg.Add(1) go func() { defer wg.Done() if err := Task(ctx); err != nil { fmt.Printf("%+v\n", err) cancel() } }() s := <-sigChan switch s { case syscall.SIGTERM: fmt.Println("!!! SIGTERM detected !!!!") cancel() // 伝搬させたcontextにキャンセルを伝える wg.Wait() // キャンセルを待つ OnAppStop() // 終了処理の実行 default: fmt.Println("unexpected signal") } } func Task(ctx context.Context) error { for i := 1; i <= 10; i++ { select { case <-ctx.Done(): return ctx.Err() case <-time.After(1 * time.Second): fmt.Printf("%d sec..\n", i) } } return nil } func OnAppStop() { fmt.Println("=== 終了処理をいろいろやる ===") fmt.Println("successful termination") }
コードをすべて反映できている訳ではないですが、概ね下記のようなシーケンスを想定しています。
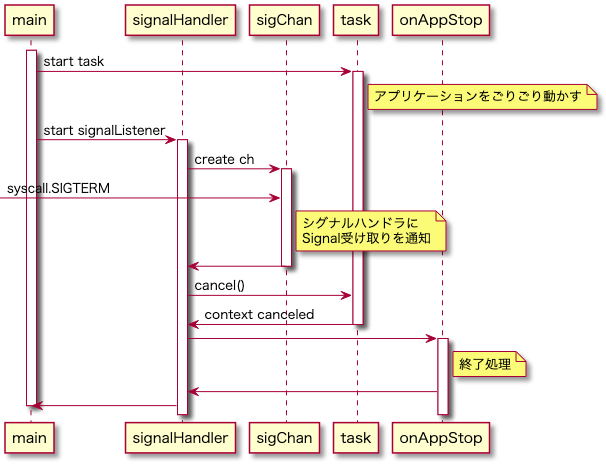
コンテキスト付きでタスクを起動し、メインゴルーチンはシグナルの受け取りを待ちます。SIGTERMをsigChanで受け取ったらコンテキストのキャンセルと終了処理を行った後、メインゴルーチン を終了します。
このコードから生成したバイナリをコンテナを実行している途中でdocker stopすると下記のようになります。
16 sec.. 17 sec.. 18 sec.. 19 sec.. 20 sec.. 21 sec.. 22 sec.. !!! SIGTERM detected !!!! context canceled === 終了処理をいろいろやる === successful termination
SIGTERMを検出したあとにcontext canceledが出力され、そのあとに終了処理を行っています。contextのキャンセルをwg.Wait()で待たせてあるので、終了処理はコンテキストのキャンセルが完了したあとに起動するようになっているためです。これで、コンテキスト内の終了処理→コンテキスト整理後の終了処理を順次行えます。
おわりに
今回は、Goでシグナルハンドリングをしながら終了処理を行う簡単なサンプルについて記事を書きました。ここでのサンプルコード以外にもさまざまな実装方法があるかと思いますが、シグナルを待つ→シグナルを受け取る→後処理の流れは変わらないと思います。みなさま是非、コンテナを安全に葬れるようなコーディングを心がけましょう。明日は @ubonsa さんです。お楽しみに!
余談
Q SIGKILLは?
A SIGKILLはハンドリングできません。ので、docker killされたら終了処理も出来ずにコンテナが死にます。
Q SIGTERMとSIGINT両方拾いたいんだが
A func signal.Notify(c chan<- os.Signal, sig ...os.Signal)では、拾いたいシステムコールを追加できます。したがって、signal.Notify(sigChan, syscall.SIGINT, syscall.SIGTERM)とすれば、二つのシステムコールのどちらかを拾うことができます。
Q: このサンプルコードだとsignal受け取らない限りメインゴルーチン終了しないよね?
A 終了しません。sigChanで待ち続けます。ですので、下記コードのようにsignalを受け取るgoroutineを別で走らせておくのがいいと思います。waitSigみたいなファンクションを切って呼びたい。
func main() { ctx, cancel := context.WithCancel(context.Background()) defer cancel() wg := sync.WaitGroup{} wg.Add(1) go func() { defer wg.Done() if err := Task(ctx); err != nil { fmt.Printf("%+v\n", err) cancel() } }() sigChan := make(chan os.Signal, 1) signal.Notify(sigChan, syscall.SIGTERM) go func() { defer close(sigChan) s := <-sigChan switch s { case syscall.SIGTERM: fmt.Println("!!! SIGTERM detected !!!!") cancel() // 伝搬させたcontextにキャンセルを伝える wg.Wait() // キャンセルを待つ OnStopApp() // 終了処理の実行 default: fmt.Println("unexpected signal") } }() wg.Wait() fmt.Println("done!") }
雑なシーケンス
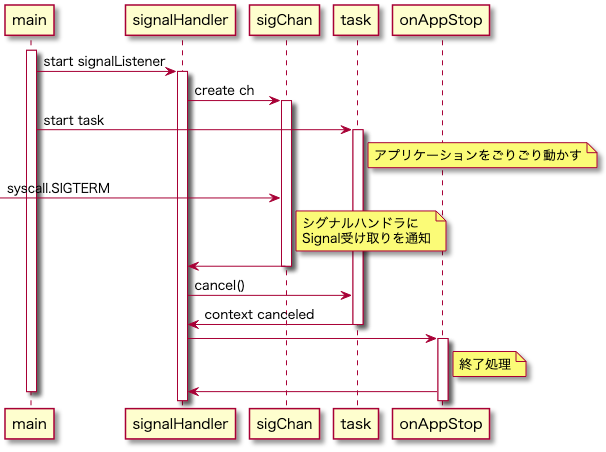
参考文献
- Amazon Elastic Container Service 開発者ガイド サービスの更新 https://docs.aws.amazon.com/ja_jp/AmazonECS/latest/developerguide/update-service.html
- Package signal https://golang.org/pkg/os/signal/
- [Go] signal.Notifyを使うときは必ずバッファ付きチャネルで利用すること https://budougumi0617.github.io/2020/09/06/why_signal_notify_want_buffered_channel/
- Amazon ECS Deep Dive - Awsstatic https://d1.awsstatic.com/webinars/jp/pdf/services/20190731_AWS-BlackBelt_AmazonECS_DeepDive_Rev.pdf
*1:ECSだけでなくkubernetesでも、podの終了処理時に同等のことをやっています。https://qiita.com/superbrothers/items/3ac78daba3560ea406b2
*2:一応、stopTimeoutというパラメータでMAX120秒までコンテナの寿命を伸ばせます。 タスク定義パラメータ - Amazon Elastic Container Service
*3:ECSのタスク更新・SIGTERM発行→SIGKILL発行まで30秒の猶予がありますから、大抵の処理は終了しているはずです。とはいったものの、外部のAPIのコールなどネットワーク遅延による大幅な遅延もなきにしもあらずですから、終了処理を書いて安全にアプリのコンテナを止めることには十分意義があると思います。仮にマイクロサービスで動いているのであれば、トランザクションのコーディネーターに対して未完了であることを伝達する必要がある盤面もあるでしょう。
*4:正確には、tx.Commit()、もしくは、tx.Rollback()がコールされると、sql.DBインスタンスから借りていたコネクションをfreeConに返す処理をしています。この辺の挙動については以下の記事が詳しいです。
*5:
strings.Joinの中身を見てみる
strings.Joinの中身を見てみる
// Join concatenates the elements of its first argument to create a single string. The separator // string sep is placed between elements in the resulting string. func Join(elems []string, sep string) string { switch len(elems) { case 0: return "" case 1: return elems[0] } n := len(sep) * (len(elems) - 1) for i := 0; i < len(elems); i++ { n += len(elems[i]) } var b Builder b.Grow(n) b.WriteString(elems[0]) for _, s := range elems[1:] { b.WriteString(sep) b.WriteString(s) } return b.String() }
早期リターン
最初に、Strings.Builferによる結合が必要がないものについてはそのまま要素を返す
switch len(elems) { case 0: return "" case 1: return elems[0] }
確保するメモリを前もって計算
Joinの第二引数であるセパレーターの要素数と、結合対象となる文字列スライスの要素数を掛け算し、必要なセパレーターの数を計算 次に文字列スライスの要素数分のだけnに加算していく。
n := len(sep) * (len(elems) - 1) for i := 0; i < len(elems); i++ { n += len(elems[i]) }
メモリの確保
var b Builder
b.Grow(n)
b.Glow(n)で先程計算したメモリ量分だけメモリ領域を拡張する。
// Grow grows b's capacity, if necessary, to guarantee space for // another n bytes. After Grow(n), at least n bytes can be written to b // without another allocation. If n is negative, Grow panics. func (b *Builder) Grow(n int) { b.copyCheck() if n < 0 { panic("strings.Builder.Grow: negative count") } if cap(b.buf)-len(b.buf) < n { b.grow(n) } }
コメント部分和訳
Grow は、必要に応じて b の容量を増やし、さらに n バイト分のスペースを保証します。Grow(n) の後、少なくとも n バイトを b に書き込むことができます。n が負の値の場合、Grow はパニックに陥ります。
メモリ領域が確保されたbuilderに対してappend
結合対象となるスライスとセパレーターの数だけメモリ領域が確保されたbuilderに対し、WriteStringを行って結合処理をする。
b.WriteString(elems[0]) for _, s := range elems[1:] { b.WriteString(sep) b.WriteString(s) } return b.String()
おまけ
strings.Join内のb.Glow(n)を外したらどうなるのか気になったので実験した。
package main import ( "fmt" "strconv" "strings" "testing" ) var slice []string func Benchmark(b *testing.B) { slice = gen(b, 1000) b.ResetTimer() BenchmarkJoin(b) } func BenchmarkJoin(b *testing.B) { fmt.Println(strings.Join(slice, " a ")) } func gen(b *testing.B, n int) []string { var slice []string for i := 0; i < n; i++ { slice = append(slice, strconv.Itoa(i)) } return slice }
b.Glow(n)を使わないようにコメントアウト
var b Builder // b.Grow(n) b.WriteString(elems[0])
結合処理全体の処理時間におけるベンチマークが以下。 実験時の条件だけ踏まえれば、b.Glow(n)の有無によるベンチマーク差がそのままappend()処理時にスライスの拡張が必要になった場合のメモリアロケーションによるベンチマーク差と一致する。
| b.Glow(n)あり | b.Glow(n)なし | 差 | |
|---|---|---|---|
| n=100 | 0.000017 ns/op | 0.000024 ns/op | 0.000007 ns/op |
| n=1000 | 0.000044 ns/op | 0.000064 ns/op | 0.000020 ns/op |
| n=10000 | 0.000221 ns/op | 0.000586 ns/op | 0.000365 ns/op |
| n=100000 | 0.008440 ns/op | 0.010600 ns/op | 0.002160 ns/op |
| n=1000000 | 0.129000 ns/op | 0.135000 ns/op | 0.006000 ns/op |
【Terraform】CloudWatchのカスタムメトリクスでログ出力をフィルタリングしてそのアラームをSlackで流したい
背景
コンテナ化に伴い、標準出力によるロギングが一般的になりました。それに伴い、ログストリームからイベントを拾い上げるような監視の仕組みが必要な場面があります。 今回、「標準出力によって吐かれたログからERRORという文字列を検出する」という要件でのアラート設計が必要になったため、特定のキーワードによるログストリームのフィルタリングを行い、キーワードが検出されればSlackに通知する仕組みをTerraformで記述しました。
環境
- Ubuntu20.04
- Terraform 0.13.4 ( tfenv v2.0.0 / tflint v0.18.0)
- aws
概要
log_group, metric_filter, metric_alarmを定義し、alarm_actionをSlack用のSNSトピックにpublish。sns_topicをchatbotでsubscribe。 chatbot用のmoduleがうまく動作しなかったため、SNSトピックまでのパイプラインを構築し、あとでSNSトピックとchatbotを紐付けます。
. ├── aws_cloudwatch_log_group.tf // 今回は使用しない ├── aws_cloudwatch_log_group_variables.tf ├── aws_cloudwatch_log_metric_filter.tf ├── aws_cloudwatch_metric_alarm.tf ├── sns.tf ├── chatbot.tf // moduleを使用しようとしたが動かなったためここだけ手動 ├── provider.tf
実装
まず、aws_cloudwatch_log_group_variables.tfにロググループのリストを定義します。このロググループのリストそれぞれに対してmetric_filterを定義し、さらに、定義したmetric_filterそれぞれに対してaws_cloudwatch_metric_alarm.tfにてアラームを設定し、アラームの通知先をSNSトピックにします。
1、対象となるlog-groupのリストを定義
今回はすでにあるlog_groupを使用します。このcloudwatch_log_groupsにMetric filtersを設定したいlog_groupを指定します。 もちろん、log_group自体もterraformで管理しているのであれば、それに対して依存関係をもたせることで実現できます。
log_groupの数は相当数あることが多いため、for_eachを使用できるよう変数として準備しておきます。 このロググループの集合に対してフィルターとアラームを設定していくことになるため、もし監視対象を増やしたい場合、このリストにロググループを追加していくことで自動的にフィルターとアラームが追加されるようになります。
variable cloudwatch_log_groups { default = [ "/aws/lambda/go-gateway-test", "/aws/lambda/gotest", ] }
2、metric_filterの定義
標準出力によって吐かれたログからERRORという文字列を検出する
こちらは、cloudwatchのMetric filtersによって実現できます。Filter patternに”ERROR”という文字列を設定するだけで可能です。もちろん、Filter patternを柔軟に設定することで、さまざまな通知が可能です。(極論、標準出力されている文字列についてはすべて検出可能であるということです。)注意点として、このFilter patternは大文字小文字を区別します。今回の要件では、すべて大文字の”ERROR”ですから問題ありませんが、”Error”や”error”といった文字列を同時に検出する場合はmetricを複数定義する必要があります。
for_eachで、先程 ここで設定する"name"と"error_alarm"がalarmとの紐付けになるため、前もって名前空間の定義を行っておくといいでしょう。
Metric filters の定義
resource "aws_cloudwatch_log_metric_filter" "error_alarm" { # for_eachを利用するためにsetにする # 本来であればlog_groupのresourceに対して依存関係をもたせる for_each = toset(var.cloudwatch_log_groups) name = "${each.key}/error" pattern = "ERROR" log_group_name = each.key metric_transformation { name = "${each.key}/error" namespace = "error_alarm" value = 1 } }
3、Metric Alarm の定義
今回は、エラーが発生次第アラームを飛ばしたいので、その要件を基に定義していきます。 下記は「”ERROR”という文字列が120秒の間に1回以上発生した場合はnortification-slackにイベントをパブリッシュする」という例です。 1以上ですので、comparison_operatorをGreaterThanOrEqualToThreshold、thresholdを1にします。また、発生数が1以上であれば通知したいので、statisticはSumにします。アラームが発生した際のパブリッシュ対象になるalarm_actionsの宛先は後述するSNSトピックのarnを指定します。
Metric filtersとの紐付けは、metric_nameとnamespaceのセットで行います。metric_nameがあっていてもnamespaceがあっていなければ紐付けができないので注意してください。
その他設定値については下記ドキュメントへ
# metric-filter.tfで定義したカスタムメトリクス用のアラーム resource "aws_cloudwatch_metric_alarm" "test-alarm" { for_each = aws_cloudwatch_log_metric_filter.error_alarm alarm_name = "${each.key}/alarm" comparison_operator = "GreaterThanOrEqualToThreshold" evaluation_periods = "1" metric_name = "${each.key}/error" namespace = "alarm/error" period = "120" statistic = "Sum" threshold = "1" alarm_description = "This metric monitors error occurence" # データ不足時のアクションを指定 insufficient_data_actions = [] # arnを指定すること alarm_actions = [aws_sns_topic.nortification-slack.arn] }
3、SNS Topic の定義
こちらはSlack通知用SNSトピックの定義です。
resource "aws_sns_topic" "nortification-slack" {
name = "nortification-slack"
}
Chatbotの定義
こちらは画面上でポチポチします。(terraform apply後でないとSNSトピックがないので注意)
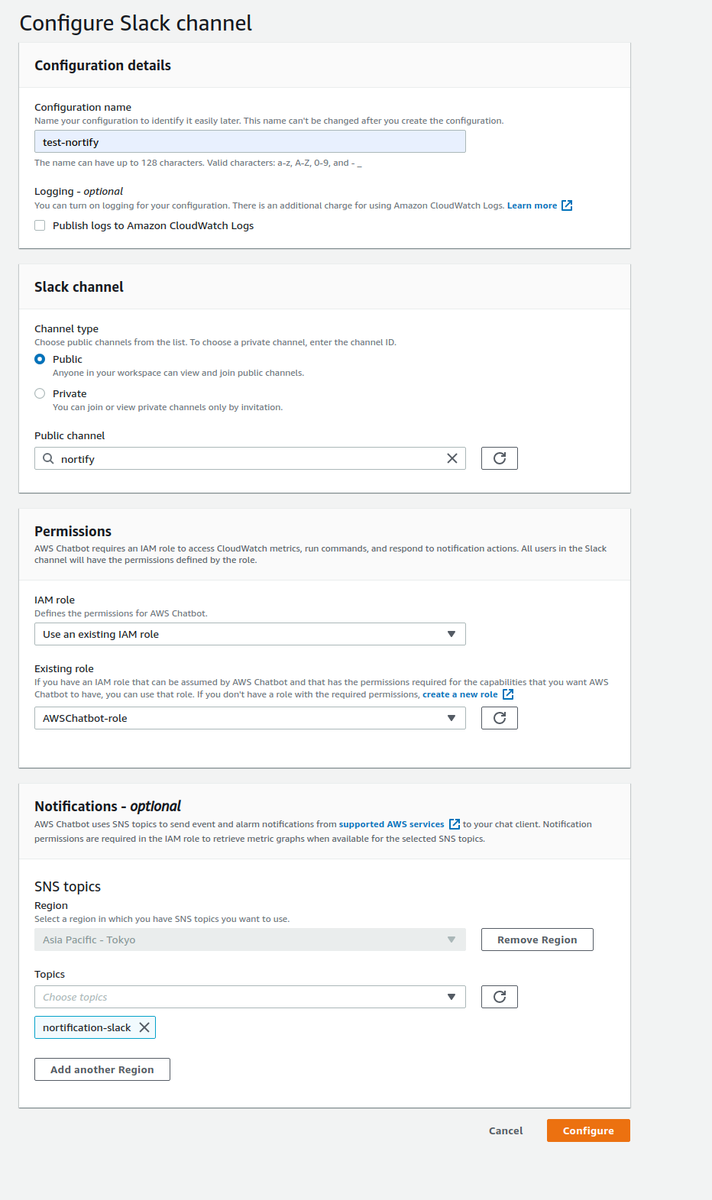
生成されたリソース
指定したロググループにフィルターが設定されています。
また、作成したメトリクスにたいしてアラームが設定されてます。
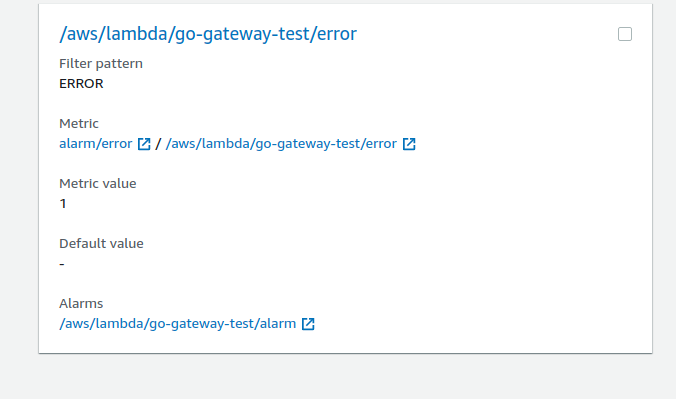
アラームは作成したSNSトピックにパブリッシュされています。
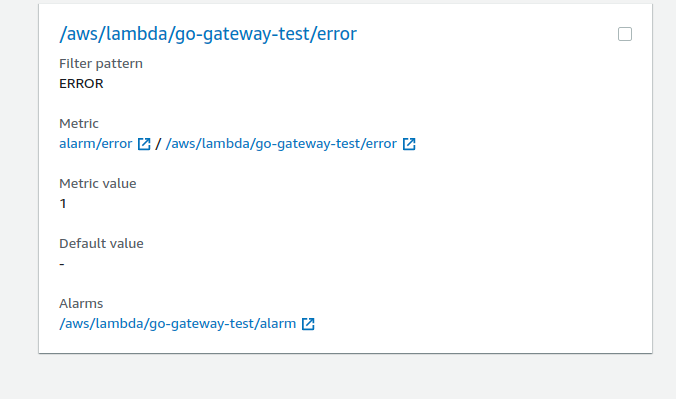

まとめ
大量のロググループに対して画面をポチポチしながらカスタムメトリクスの設定をするのは骨が折れる作業でしたので、一回コード化してしまえばかなり楽だと感じています。
ただし、監視しやすくするほど監視しすぎることが問題になるので、大量にメトリクスとアラームを作るのはやめましょう
containerd1.3.6でgo mod起因によるundedinedエラーが発生する場合における一時的なエラー回避方法
TL;DR
このエラーは
# github.com/containerd/containerd/images/archive ../../../pkg/mod/github.com/containerd/containerd@v1.3.6/images/archive/reference.go:73:21: undefined: "github.com/docker/distribution/reference".ParseDockerRef
これを消して
github.com/docker/distribution v2.7.1+incompatible // indirect
これを追加
github.com/docker/distribution v2.7.1-0.20190205005809-0d3efadf0154+incompatible // indirect
動かそうとしたソースコード
package main import ( "context" "log" "github.com/containerd/containerd" "github.com/containerd/containerd/namespaces" ) func main() { if err := redisExample(); err != nil { log.Fatal(err) } } func redisExample() error { client, err := containerd.New("/run/containerd/containerd.sock") if err != nil { return err } defer client.Close() ctx := namespaces.WithNamespace(context.Background(), "example") image, err := client.Pull(ctx, "docker.io/library/redis:alpine", containerd.WithPullUnpack) if err != nil { return err } log.Printf("Successfully pulled %s image\n", image.Name()) return nil }
事象
ビルド時に以下のエラーが発生
# github.com/containerd/containerd/images/archive ../../../pkg/mod/github.com/containerd/containerd@v1.3.6/images/archive/reference.go:73:21: undefined: "github.com/docker/distribution/reference".ParseDockerRef
原因
import (
"strings"
"github.com/containerd/containerd/reference"
distref "github.com/docker/distribution/reference" //
"github.com/opencontainers/go-digest"
"github.com/pkg/errors"
)
func normalizeReference(ref string) (string, error) {
// TODO: Replace this function to not depend on reference package
normalized, err := distref.ParseDockerRef(ref)
if err != nil {
return "", errors.Wrapf(err, "normalize image ref %q", ref)
}
return normalized.String(), nil
}
確かに、distref.ParseDockerRef(ref)は存在しなかった (そして意味深なTODO、、、、reference packageに依存しないようにしたいらしい)
一時的な回避方法。
とりあえずParseDockerRef()が存在しているリビジョンを指定してgo.modに追加
これを消して
github.com/docker/distribution v2.7.1+incompatible // indirect
これを追加
github.com/docker/distribution v2.7.1-0.20190205005809-0d3efadf0154+incompatible // indirect
AWSソリューションアーキテクトアソシエイトに合格したのでまとめる
TL;DR
- 受かるだけならWEB問題集だけで受かる
- 実践Terraformはいいぞ
スコア
- 761でした。ぎりぎりです(合格点720)
前提知識
- 自前のAWSアカウント:あり
- 業務でのAWS利用:CodeCommitとLambdaは使っているけど、他はほぼ利用しない(Lambdaのロールを付与するときにポリシーの中身確認するくらい)
- その他資格:基本情報持っている程度
- AWSまわりの勉強会の参加:AWSのサーバーレスまわりの勉強会とコンテナ系(Kube Tokyoとか)見る。
教材
WEBの問題集。ゴールドプランにしました。 aws.koiwaclub.com
実践Terraform
- kindle unlimitedで無料だったのでさらっと読みました。

Amazon Web Services ネットワーク入門 (impress top gear)
- 作者:大澤 文孝
- 発売日: 2016/11/11
- メディア: 単行本(ソフトカバー)
勉強時間の確保
緊急事態宣言があけて出社していたので、その通勤時間の30分に上述したWEBの問題集を解いていました。 1ヶ月ずっとそんな感じです。
勉強内容
WEB問題集をずーっとやってました。一応132まで1周したと思います。 体験記に80から130まで完璧にしてねと書いてあったので、前日からはそこをループしていました。
問題を解くときは以下のことだけ気をつけてました
- とりあえず解く
- 解いてすぐ解きなおす
- 7/7になるまでそのセクションを解く
AWSのサービスが多すぎるため、いったん単語なりなんなりを叩き込んで、そのあとに紐付けを行わないと永遠に終わりません。 もちろん、腰を据えて一つ一つ理解したほうがいいと思いますが、きっと忘れるので、業務や趣味で必要になったタイミングで引き出せるようにするほうがいいと思います。
ポイント:実践Terraformはいいぞ
WEB問題集以外に、なんとなく面白そうだったのでTerraformに入門していました。
結論、すごいよかったです
直接試験対策になるようなものではありませんが*1、それぞれのAWSリソースの関連図がしっかりインプットされていないと、HCLを書いていても「何を」「なんのために」書いているのかわかりません。 その関連図を、Terraformからリソースを定義することによって再構築できたので、とても勉強になりました。もちろんTerraformも少し書けるようになりました。
所感
受かったはいいけれど、ぜんぜん物足りないです。
いろいろ反省点ありますが、AWSの膨大なサービスのうち主要なものを理解して、ちゃんとAWSのアーキテクチャのことを考えられるようになったのはとてもよかったです。次はたぶんデベロッパー受けます。
余談
新宿Lタワー、ペンのインクの偏りがすごい。
*1:CloudFormation関連の問題の対策にはなるかも
【grpc】not found or had errors との戦い in Ubuntu
TL;DR
$ sudo apt install golang-goprotobuf-dev
